Расчеты изменения скорости реакции

 

 

 

 

Задача 331. 
Реакция между веществами А и В выражается уравнением: А + 2В → С. Начальные концентрации составляют: [А]₀ = 0,03 моль/л, [В]0 = 0,05 моль/л. Константа скорости реакции равна 0,4. Найти начальную скорость реакции и скорость реакции по истечении некоторого времени, когда концентрация вещества А уменьшится на 0,01 моль/л.
Решение:
До изменения концентрации скорость реакции можно выразить уравнением:

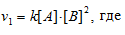
v - скорость реакции, k - константа скорости реакции, [А] и [В] – концентрации исходных веществ.

Тогда 

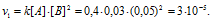
Для нахождения скорости реакции по истечении некоторого времени учтём, что на образование 1 моля вещества С затрачивается 1 моль вещества А и 2 моля вещества В, поэтому при уменьшении концентрации вещества А на 0,01 моль/л, концентрация вещества В уменьшится соответственно на 0,02 моль/л (2 ^. 0.01 = 0,02). Тогда оставшиеся концентрации веществ будут равны [A]_ост. = 0.03 – 0,01 = 0,02 моль/л, [B]_ост. = 0,05 – 0,02 = 0,03моль/л. Тогда скорость реакции по истечении некоторого времени будет составлять:

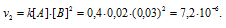
Ответ: v₁ = 3 ^. 10^-5; v₂ = 7,2 ^. 10^-6.   

---

Задача 332. 
Как изменится скорость реакции 2NO _(г.) + O_{2 (г.)} → 2NO_{2 (г.)}, если: а) увеличить давление в системе в 3 раза; б) уменьшить объем системы в 3 раза; в) повысить концентрацию в 3 раза?
Решение:
До изменения объёма, давления и концентрации скорость реакции можно выразить уравнением:

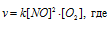
v - скорость реакции, k - константа скорости реакции, [NO] и [O₂] – концентрации исходных веществ.

а) Вследствие увеличения давления в системе в 3 раза, соответственно концентрация каждого из реагирующих веществ возрастёт в 3 раза. Следовательно, теперь скорость реакции будет равна:

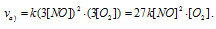
Тогда, сравнивая  выражения v  и v_а) , находим, что скорость реакции возрастает в 27 раз 

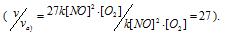
б) при уменьшении объёма в 3 раза в системе концентрация каждого из реагирующих веществ возрастёт в 3 раза. Следовательно, теперь скорость реакции будет равна:

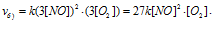
Тогда, сравнивая  выражения v  и  v_б), находим, что скорость реакции возрастает в 27 раз   

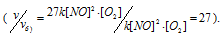
в) При увеличении концентрации NO в 3 раза скорость реакции будет равна:

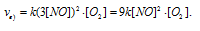
Cравнивая выражения v  и  v_в), находим, что скорость реакции возрастает в 9 раз     

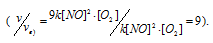
Ответ: а) возрастёт в 27 раз; б) возрастёт в 27 раз; в) возрастёт в 9 раз.

---

Задача 333. 
Две реакции протекают при 25 °С с одинаковой скоростью. Температурный коэффициент скорости первой реакции равен 2,0, а второй 2,5. Найти отношение скоростей этих реакций при 95 °С.
Решение:
Зависимость скорости реакции (или константы скорости реакции) от температуры может быть выражена уравнением:

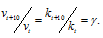
Здесь v_t и k_t - скорость и константа скорости реакции при температуре t °С; v_{(t + 10)}  и k_{(t + 10)}  те же величины при температуре (t + 10 °С); 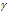 - температурный коэффициент скорости реакции, значение которого для большинства реакций лежит в пределах 2 - 4 (правило Вант-Гоффа). В общем случае, если температура изменилась на 95 °С, последнее уравнение преобразуется к виду:   

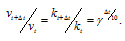
Поскольку 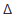t = 70 °С (95 – 25 = 75), то, скорость реакции равна: 

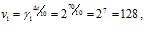
Скорость второй реакции равна:

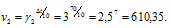
Найдём отношение этих скоростей:

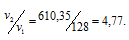
Ответ: 4,77.

---

 Задача 334. 
Чему равен температурный коэффициент скорости реакции, если при увеличении температуры на 30 градусов скорость реакции возрастает в 15,6 раза?
Решение:
Согласно правилу Вант Гоффа зависимость скорости реакции от температуры выражается уравнением:

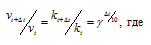
v_t  и k_t - скорость и константа скорости реакции при температуре t °С; v_{(t + 10)}  и k_{(t + 10)} те же величины при температуре (t + 10 °С); 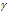- температурный коэффициент скорости реакции, значение которого для большинства реакций лежит в пределах 2 – 4. Поскольку 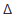t = 30 °С, то, подставив в уравнение Вант-Гоффа значения по условию задачи, рассчитаем температурный коэффициент скорости реакции:

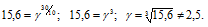
Ответ: 2,5.

---

Задача 335. 
Температурный коэффициент скорости некоторой реакции равен 2,3. Во сколько раз увеличится скорость этой реакции, если повысить температуру на 25 градусов?
Решение:
Согласно правилу Вант Гоффа зависимость скорости реакции от температуры выражается уравнением:

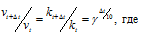
v_t и k_t - скорость и константа скорости реакции при температуре t °С; v_{(t + 10)}  и k_{(t + 10)} те же величины при температуре (t + 10 °С); 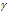 - температурный коэффициент скорости реакции, значение которого для большинства реакций лежит в пределах 2 – 4. Поскольку 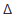t = 25 °С, то, обозначив скорость начальной реакции и скорость реакции при повышении температуры системы на 25 градусов соответственно через v  и  v', можем записать:

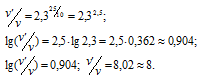
Ответ: в 8 раз.                     

---