Вычисление константы равновесия химических реакций
Задача 675.
Пользуясь таблицей стандартных электродных потенциалов, вычислить константы равновесия следующих реакций:
а) Zn + CuSO4 = Cu + ZnSO4;
б) Sn + Pb(CH3COO)2 = Sn(CH3COO)2+ Pb.
Решение:
а) Zn + CuSO4 = Cu + ZnSO4
Составляем уравнения электронного баланса:
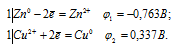
Для определения ЭДС гальванического элемента необходимо из потенциала катода вычесть потенциал анода, т.е. при вычислении ЭДС элемента меньший электродный потенциал вычитается из большего (в алгебраическом смысле), получим:
EЭДС = E(Cu0) - E(Zn0) =
= 0,337 - (-0,763) = 1,1 B.
Константу равновесия процесса находим по уравнению:
lgK = (nЕЭДС)/0,059 = (2 . 1,1)/0,059 =
= 37,288; K = 1,94 . 1037.
Здесь n – число электронов, принимающих участие в процессе.
б) Sn + Pb(CH3COO)2 = Sn(CH3COO)2+ Pb
Составляем уравнения электронного баланса:
1|Sn0 - 2e = Sn2+, E° = -0,136 B;
1|Pb2+ + 2e = Pb0, E° = -0,126 B.
EЭДС = E(Pb0) - E(Sn0) =
= 0,126 - (-0,136) = 0,1 B.
lgK = (nЕЭДС)/0,059 = (2 . 0,1)/0,059 =
= 3,39; K = 2,45 . 103.
Здесь n – число электронов, принимающих участие в процессе.
Ответ: а) 1,94 . 1037; б) 2,45 . 103.
Задача 676.
Вычислить константы равновесия реакций, протекающих
а) в кадмиево-цинковом гальваническом элементе; 6) в медно-свинцовом гальваническом элементе.
Решение:
а) Составляем уравнения электронного баланса:
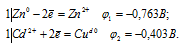
Для определения ЭДС гальванического элемента необходимо из потенциала катода вы-честь потенциал анода, т.е. при вычислении ЭДС элемента меньший электродный потенциал вычитается из большего (в алгебраическом смысле), получим:
EЭДС = E(Cd0) - E(Zn0) =
= -0,403 - (-0,763) = 0,360 B.
Константу равновесия процесса находим по уравнению:
lgK = (nЕЭДС)/0,059 = (2 . 0,36)/0,059 = 12,20; K = 1,58 . 1012.
Здесь n – число электронов, принимающих участие в процессе.
а) Составляем уравнения электронного баланса:
1|Pb0 - 2e = Pb2+, E° = -0,126 B;
1|Cu2+ + 2e = Cu0, E° = 0,337 B.
EЭДС = E(Cu0) - E(Pb0) =
= 0,337 - (-0,126) = 0,463 B.
Константу равновесия процесса находим по уравнению:
lgK = (nЕЭДС)/0,059 = (2 . 0,463)/0,059 =
= 15,695; K = 4,95 . 1015.
Здесь n – число электронов, принимающих участие в процессе.
Ответ: а) 1,58 . 1031; б) 2,018 . 1015.
Задача 677.
Можно ли восстановить олово (IV) в олово (II) с помощью следующих реакций:
а) SnCl4 + 2KI = SnCl2 + 2KCl;
б) SnCl4+ 2H2S = SnCl2 + S + 2HCl.
Ответ обосновать расчетом констант равновесия реакций.
Решение:
а) SnCl4 + 2KI = SnCl2 + 2KC
Составляем уравнения электронного баланса:
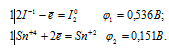
Для определения ЭДС гальванического элемента необходимо из потенциала катода вы-честь потенциал анода, т.е. при вычислении ЭДС элемента меньший электродный потенциал вычитается из большего (в алгебраическом смысле), получим:
EЭДС = E(Sn0) - E(I20) =
= 0,151 - 0,536 = -0,385 B.
Константу равновесия процесса находим по уравнению:
lgK = (nЕЭДС)/0,059 = 2 (-0,385)/0,059 =
= -13,05; K = 8,91 . 10-14.
Здесь n – число электронов, принимающих участие в процессе.
Вывод:
Так как константа равновесия реакции К < 0, то процесс не протекает самопроизвольно при нормальных условиях.
б) SnCl4+ 2H2S = SnCl2 + S + 2HCl.
Составляем уравнения электронного баланса:
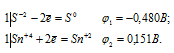
Для определения ЭДС гальванического элемента необходимо из потенциала катода вы-честь потенциал анода, т. е. при вычислении ЭДС элемента меньший электродный потенциал вычитается из большего (в алгебраическом смысле), получим:
EЭДС = E(Sn0) - E(S) =
= 0,151 - (-o,481) = 0,631 B.
Константу равновесия процесса находим по уравнению:
lgK = (nЕЭДС)/0,059 = 2(0,631)/0,059 =
= 21,39; K = 2,45 . 1021.
Выводы: Так как константа равновесия реакции K > 0, то процесс протекает самопроизвольно при нормальных условиях.
Ответ: а) нельзя, К = 8,91 . 10-14; б) можно, К = 2,45 . 1021.

