Расчеты при решении химико-экономических задач

 

 

 

 

Необходимо уметь рассчитывать массовые доли продуктов питания и лечебных препаратов. Интересно отметить, что пищевой продукт, продающийся в магазинах под торговой маркой «уксус», представляет собой раствор уксусной кислоты в воде. Причем на этикетке указывается массовая доля уксусной кислоты. Чаще всего «уксус» бывает 6% или 9%. Но иногда можно встретить в магазине «уксусную эссенцию». На этикетке этого продукта указана массовая доля уксусной кислоты — 70% . Для выяснения вопроса, какой из продуктов наиболее выгодно покупать (все эти продукты налиты в разную тару и имеют различную цену) необходимо уметь рассчитывать массу чистого уксуса в любом из этих растворов.

Задача 1. 
В магазине на полке стоят три разных раствора уксусной кислоты. Ценник под каждым из продуктов выглядит следующим образом: 
масса первого продукта: m_1р-ра = 0,5 кг;
массовая доля уксусной кислоты в первом продукте: ₁(CH₃COOH) = 6% ;
цена первого продукта: 20 руб.;
масса второго продукта: m_2р-ра = 300 г;
массовая доля уксусной кислоты во втором продукте: ₂(CH₃COOH) = 9%;
цена второго продукта: 15 руб.;
масса третьего продукта: m_3р-ра = 300 г;
массовая доля уксусной кислоты в третьем продукте: 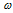₃(CH₃COOH) = 70%;
цена третьего продукта: 40 руб.
Определите, какая покупка будет наиболее выгодной.
Решение:
Покупая любой из этих продуктов, мы платим только за уксусную кислоту. Налить воду из крана и сделать раствор можно дома. Поэтому для выявления наиболее выгодной покупки необходимо вычислить содержание уксусной кислоты в каждом из растворов и только затем сравнить стоимость.

Схематично алгоритм решения можно представить следующим образом:

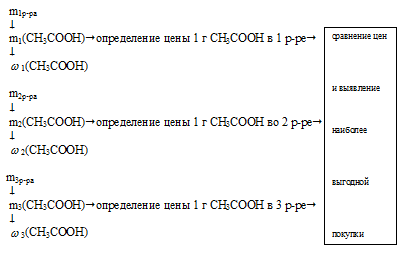
1. Определим массу чистой уксусной кислоты в 0,5 кг 6% раствора. Это можно сделать по соотношению:

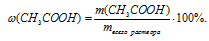
Подставляем известные нам данные, получим:

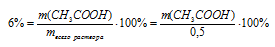
Находим из этого уравнения массу чистой уксусной кислоты:

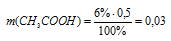
m₁(CH₃COOН) = 0,03 кг (т.к. масса раствора была выражена в килограммах).

Для сравнения более удобно перевести килограммы в граммы, так как масса остальных растворов выражена в граммах: m₁(CH₃COOН) = 30 г.

30 г СН₃СООН содержится в 0,5 кг 6% -ного раствора.

Можно было посчитать не только по соотношению, но и используя пропорцию:

0,5 кг раствора составляют 100%
х кг уксусной кислоты составляют 6%

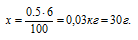
При самостоятельном решении задач можно использовать любой способ.

2. Определим массу чистой уксусной кислоты в 300 г 9% раствора:

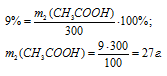
m₂ (СН₃СООН) = 27 г (содержится в 300 г 9% раствора).

3. Определим массу чистой уксусной кислоты в 170 г 70% раствора:

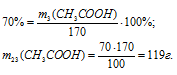
m₃ (СН₃СООН) =119 г (содержится в 170 г 70%-ного раствора).

Теперь приступим к экономической части задачи. Сопоставляя вычисленные массы чистой уксусной кислоты с ценой раствора, получаем:

30 г уксусной кислоты (6% раствор) стоят 20 руб.
27 г уксусной кислоты (9% раствор) стоят 15 руб.
119 г уксусной кислоты (70% раствор) стоят 40 руб.

Для сравнения и выбора наиболее выгодного варианта необходимо определить стоимость 1 г уксусной кислоты в каждом из растворов при помощи составления и решения пропорций, оформив их в виде таблицы:

Для 6% -ного раствора	Для 9% -ного раствора	Для 70% -ного раствора
30 г стоят 20 руб.; 1 г стоит х руб.	27 г стоят 15 руб.; 1 г стоит х руб.	119 г стоят 40 руб.; 1 г стоит х руб.
х = 20 . 1/30 = 0,67руб.	х = 15 . 1/27 = 0,56руб.	х = 40 . 1/119 = 0,37руб.

Из полученных данных видно, что покупка уксусной эссенции (70% -ного раствора) будет наиболее выгодной¹.

Ответ:  с экономической точки зрения, покупка 170 г 70% - ной уксусной эссенции будет наиболее выгодной, т.к. в этом растворе стоимость уксусной кислоты минимальна.

---

Комментарии:
¹Полученный ответ верен только для случая соотношения цен и растворов, указанных в условии. Для других вариантов может получиться иной ответ.  

---