Расчет массовой доли, температуры кристаллизации и кипения растворов неэлектролитов
Молярная масса растворенного вещества
Задание 161.
Раствор, содержащий 0,512 г неэлектролита в 100 г бензола, кристаллизуется при 5,296 °С. Температура кристаллизации бензола 5,5 °С. Криоскопическая константа 5,1°. Вычислите молярную массу растворенного вещества. Ответ: 128 г/моль.
Решение:
Понижение температуры кристаллизации вещества равно:
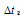= 5,5 – 5,26 = 0,2040.
Масса растворённого вещества, приходящегося на 1000 г бензола равна:
m(бензол) = (0,512 . 1000)/100 = 5,12 г.
Для расчета молекулярной массы вещества используем уравнение:
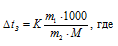
К – криоскопическая константа; m1 – масса растворённого вещества; m2 – масса растворителя; М – молярная масса растворённого вещества; 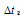– понижение температуры замерзания раствора.
Тогда
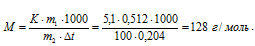
Ответ: 128 г/моль.
Массовая доля раствора
Задание 162.
Вычислите массовую долю (%) водного раствора сахара С12Н22О11 зная, что температура кристаллизации раствора -0,93 °С. Криоскопическая константа воды 1,86°. Ответ: 14,6%.
Решение:
Температура кристаллизации чистой воды равна 0 oС, следовательно,
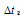= 0 - (-0,93) = +0,930.
МС12Н22О11 = 342 г/моль. Находим массу С12Н22О11, приходящуюся на 1000 г воды используя формулу:
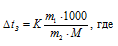
К – криоскопическая константа; m1 – масса растворённого вещества; m2 – масса растворителя; М – молярная масса растворённого вещества; 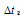– понижение температуры замерзания раствора.
Тогда с учётом того, что m2 равно 1000 г, получим:
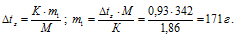
Общая масса раствора, содержащего 171 г сахара, составляет 1000 + 171 = 1171 г. Процентное содержание сахара в данном растворе находим из соотношения:
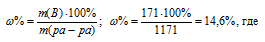
m(B) – масса растворённого вещества m(смеси); m(ра-ра) – масса раствора, которая составляет сумму масс растворителя и растворённого вещества [m(ра-ра) = m(ра-ля) + m(В); - массовая доля растворённого вещества в процентах.
Ответ: 14,6%.
Температура кристаллизации раствора
Задание 163.
Вычислите температуру кристаллизации раствора мочевины (NH2)2CO, содержащего 5 г мочевины в 150 г воды. Криоскопическая константа воды 1,86°. Ответ: -1,03 °С.
Решение:
М((NH2)2CO) = 60 г/моль.
По закону Рауля понижение температуры кристаллизации и повышение температуры кипения раствора (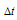
) по сравнению с температурами кристаллизации и кипения растворителя выражаются уравнениями:
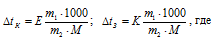
Е – эбуллиоскопическая константа; К – криоскопическая константа; m1 – масса растворённого вещества; m2 – масса растворителя; М – молярная масса растворённого вещества; 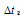– понижение температуры замерзания раствора. Тогда понижение температуры кристаллизации раствора мочевины равно:
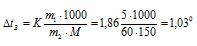
Вода кристаллизуется при 0 оС, следовательно, температура кристаллизации раствора мочевины равна:
Тз = 0 – 1,03 = -1,03 oС.
Ответ: -1,03 °С.
Эбулиоскопическая константа
Задание 164.
Раствор, содержащий 3,04 г камфоры С10Н16О в 100 г бензола, кипит при 80,714 °С. Температура кипения бензола равна +80,2 °С. Вычислите эбулиоскопическую константу бензола. Ответ: 2,57.
Решение:
Повышение температуры кипения равно:
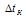= 80,714 – 80,2 =
= 0,5140. М(С10Н16О) = 152 г/моль.
Эбулиоскопическую константу камфоры вычислим, используя уравнение Рауля:
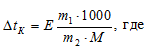
Е – эбулиоскопическая константа; m1 – масса растворённого вещества; m2 – масса растворителя; М – молярная масса растворённого вещества; 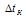– повышение температуры кипения раствора.
Отсюда
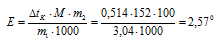
Ответ: 2,57 °С.
Массовая доля раствора
Задание 165.
Вычислите массовую долю (%) водного раствора глицерина С3Н5(ОН)3, зная, что этот раствор кипит при 100,39 °С. Эбулиоскопическая константа воды 0.52°. Ответ: 6,45%.
Решение:
М[(С3Н5(ОН)3] = 92 г/моль.
Температура кипения чистой воды равна 100 °С, следовательно:
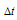= 100,39 - 100 = +0,390.
Находим массу С3Н5(ОН)3 приходящуюся на 1000 г воды используя формулу:
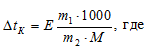
Е – эбулиоскопическая константа; m1 – масса растворённого вещества; m2 – масса растворителя; М – молярная масса растворённого вещества; 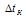– повышение температуры кипения раствора.
Тогда с учётом того, что m2 равно 1000 г, получим:
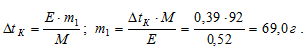
Общая масса раствора, содержащего 69,0 г глицерина, составляет 1000 + 69,0 = 1069,0 г. Процентное содержание глицерина в данном растворе находим из соотношения:
w% = (m(B) . 100%)/m(ра-ра) =
= (69,0 . 100% )/1069,0 = 6,45%.
m(B) – масса растворённого вещества m(смеси); m(ра-ра) – масса раствора, которая составляет сумму масс растворителя и растворённого вещества [m(ра-ра) = m(ра-ля) + m(В);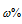 
- массовая доля растворённого вещества в процентах.
Ответ: 6,45%.
Молярная масса неэлектролита
Задание 166.
Вычислите молярную массу неэлектролита, зная, что раствор, содержащий 2,25 г этого вещества в 250 г воды. кристаллизуется при -0,279 °С, Криоскопическая константа воды 1,86°. Ответ: 60 г/моль.
Решение:
Температура кристаллизации чистой воды равна 0 oС, следовательно,
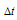= 0 - (-0,279) = +0,2790.
Для расчета используем уравнение:
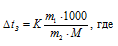
К – криоскопическая константа; m1 – масса растворённого вещества; m2 – масса растворителя; М – молярная масса растворённого вещества; 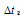– понижение температуры замерзания раствора.
Тогда
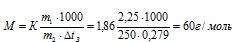
Ответ: 60 г/моль.
Температура кипения раствора
Задание 167.
Вычислите температуру кипения 5%-ного раствора нафталина С10Н8 в бензоле. Температура кипения бензола 80,2 oС. Эбулиоскопическая константа его 2,57°. Ответ: 81,25 °С.
Решение:
М(С10Н8) = 128 г/моль.
По закону Рауля раствор закипает при более высокой температуре, так как концентрация молекул растворителя в нём всегда ниже, чем в чистом растворителе, и давление насыщенного пара раствора достигает атмосферного при более высокой температуре. Выражается это уравнением:
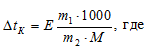
Е – эбулиоскопическая константа; m1 – масса растворённого вещества, 5 г; m2 – масса растворителя 95 г; М – молярная масса растворённого вещества; 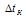– понижение температуры замерзания раствора.
Повышение температуры кипения раствора нафталина равно:
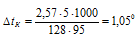
Следовательно, температура кипения раствора:
t(ра-ра) = t(ра-ля) + =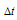
= 80,2 + 1,05 = 81,25 oС.
Ответ: 81 ,25 °С.
