Решение задач с использованием уравнения состояния идеального газа
Задача 90.
Какой объем займет 1 кг воздуха при 17 °С и давлении 101,33 кПа?
Решение:
Выразив данные задачи в системе единиц СИ (Р = 10,133 . 104 Па; m = 1кг; Т = 290 К) и подставив их, с учётом, что мольная масса воздуха равна 29 г/моль, в уравнение Клапейрона- Менделеева (уравнение состояния идеального газа), находим мольную массу газа:
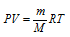
Здесь
R – универсальная газовая постоянная, равная 8,314 Дж/(моль . К); Т – температура газа, К; Р – давление газа, Па; V – объём газа, м3; М – мольная масса газа, г/моль.
Отсюда
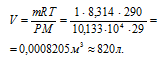
Ответ :V(Возд.) 820 л.
Задача 91.
Газометр вместимостью 20 л наполнен газом. Плотность этого газа по воздуху 0,40, давление 103,3 кПа (774,8 мм. рт. ст.), температура 17 °С. Вычислить массу газа.
Решение:
Мольную массу газа находим по формуле:
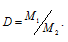
Здесь
D - плотность газа по воздуху; M1 - мольная масса газа; M2 - мольная масса воздуха (29 г/моль). Тогда
M1 = D . M2 = 6,92 . 29 = 200,6 г/моль.
Выразив данные задачи в системе единиц СИ (Р = 10,33 . 104 Па; V = 2 . 10-5; Т = 290 К) и подставив их, с учётом, что мольная масса воздуха равна 29 г/моль, в уравнение Клапейрона- Менделеева (уравнение состояния идеального газа), находим мольную массу газа:
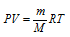
Здесь
R – универсальная газовая постоянная, равная 8,314 Дж/(моль . К); Т – температура газа, К; Р – давление газа, Па; V – объём газа, м3; М – мольная масса газа, г/моль.
Отсюда
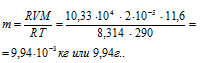
Ответ: m(Газа) = 9,94 г.
Задача 92.
Масса колбы вместимостью 750 мл, наполненной при 27 °С кислородом, равна 83,3 г. Масса пустой колбы составляет 82,1 г. Определить давление кислорода.
Решение:
Находим массу кислорода в колбе:
m = 83,3 - 82,1 = 1,2 г.
Мольная масса кислорода равна = 32 г/моль.
Выразив данные задачи в системе единиц СИ и подставив их в уравнение Клапейрона- Менделеева (уравнение состояния идеального газа), давление газа:
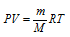
Здесь
R – универсальная газовая постоянная, равная 8,314 Дж/(моль . К); Т – температура газа, К; Р – давление газа, Па; V – объём газа, м3; М – мольная масса газа, г/моль.
Отсюда
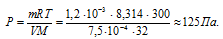
Ответ: = 125 Па.
Задача 93.
Вычислить массу 1 м3 воздуха при 17 °С и давлении 83,2 кПа (624 мм рт. ст.).
Решение:
Мольная масса воздуха равна = 29 г/моль.
Выразив данные задачи в системе единиц СИ и подставив их в уравнение Клапейрона- Менделеева (уравнение состояния идеального газа), давление газа:
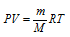
Здесь
R – универсальная газовая постоянная, равная 8,314 Дж/(моль . К); Т – температура газа, К; Р – давление газа, Па; V – объём газа, м3; М – мольная масса газа, г/моль.
Отсюда
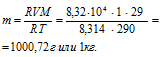
Ответ: m(Возд.) = 1 кг.
Задача 94.
Какой из перечисленных ниже фактов может служить доказательством одноатомности газообразного неона: а) неон не образует соединений с другими элементами; б) плотность вдвое меньше, чем плотность следующего благородного газа — аргона; в) плотность неона почти вдвое меньше плотности фтора — предыдущего элемента периодической системы?
Решение:
а) Все инертные газы не образуют соединений с другими элементами, поэтому этот факт не служит доказательством одноатомности молекулы неона;
б) Известно, что аргон имеет атомную массу в два раза большую, чем неон, но это не может быть доказательством одноатомности молекулы неона;
в) Известно, что фтор образует простое вещество, состоящее из двухатомных молекул F2 с молярной массой 32г/моль.
Из закона Авогадро следует, что
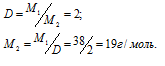
Молекулярная масса, найденная по расчету приблизительно соответствует атомной массе неона 20,18 г/моль, т.е. – количество атомов неона в молекуле равно приблизительно единице.
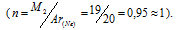
Из чего вытекает, что газообразный неон имеет одноатомное строение.
Ответ: в).
Задача 95.
Чему равна плотность хлора по воздуху: а) 2,44; 6) 3,0; в) можно определить только опытным путем?
Решение:
Молекулярная масса хлора равна 71 г/моль, воздуха равна 29 г/моль.
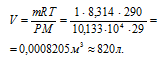
Ответ: а).
Задача 96.
Газообразный оксид содержит 30,4% азота. В молекулу оксида входит один атом азота. Чему равна плотность газа по кислороду: а) 0,94; 6) 1,44; в) 1,50?
Решение:
Молекулярная масса кислорода равна 32 г/моль.
Молекула оксида содержит один атом азота, что составляет 30,4%. Зная, что атомная масса азота составляет 14 г/моль можно вычислить молекулярную массу оксида из пропорции:
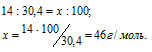
Из закона Авогадро следует, что при одном и том давлении и одинаковых температуре массы равных объёмов газов относятся как их молекулярные массы:
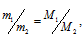
где
m1/m2 - относительная плотность первого газа по второму, обозначаемая D. Следовательно:
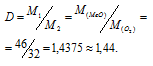
Ответ: в).
Задача 97.
Масса 2,24 л газа (условия нормальные) равна 2,8 г. Чему равна молекулярная масса газа: а) 14; 6) 28; в) 42?
Решение:
При нормальных условиях 1 моль любого газа занимает объём 22,4 л Вычислив массу 22,4 л данного газа, мы узнаем его мольную массу из пропорции:
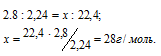
Мольная масса вещества численно равна его молекулярной массе. Следовательно, молекулярная масса данного газа равна 28.
Ответ: M(Газ) = 28 г/моль.
Задача 98.
Масса атома серы в два раза больше массы атома кислорода. Можно ли на этом основании считать, что плотность паров серы по кислороду равна двум: а) можно; б) нельзя?
Решение:
Из закона Авогадро следует, что при одном и том давлении и одинаковых температуре массы равных объёмов газов относятся как их молекулярные массы:
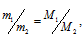
где
m1/m2 - относительная плотность первого газа по второму, обозначаемая D. Следовательно:
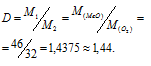
Таким образом, плотность первого газа по второму определяется отношением их мольных масс. Поэтому считать, что плотность паров серы по кислороду равна двум нельзя, так как их атомные массы не относятся как 2/1. Молекула кислорода состоит из двух атомов а молекула серы состоит из восьми атомов Следовательно, относительная плотность паров серы (D) по кислороду равна 8:
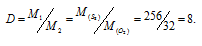
Здесь
М1 – молекулярная масса серы 256 г/моль [M(S8) = Ar(S8) =8 . 32 = 256], а М2 – молекулярная масса кислорода 32 г/моль
Таким образом, считать, что плотность паров серы по кислороду равна 2 нельзя.
Ответ: б).

